
Part 1: The P2D Model, The Cell Model
Lithium-ion batteries, characterized by high energy density, large power output, and rapid charge–discharge rates, have become one of the most widely used rechargeable electrochemical energy storage devices. They find extensive applications in various domains such as electronic products, electric vehicles, and grid energy storage systems.
However, the lithium-ion batteries primarily consist of flammable electrolytes and active electrode materials, under high temperature abuse or accidental conditions, the batteries may undergo thermal runaway due to exothermic reactions, potentially leading to fire incidents.
To prevent accidents, it is crucial to conduct safety testing and screening on the commercial lithium-ion batteries. Currently, common detection methods for lithium-ion batteries include disassembly characterization methods and in-situ characterization methods. Disassembly methods, such as scanning electron microscopy (SEM) provide rich information about battery material properties.
However, they may alter the internal structure during disassembly, leading to less accurate information. Moreover, invasive detection methods like disassembly can disrupt the battery structure, making it difficult to obtain accurate fault information. In-situ characterization methods, such as X-ray CT scanning offer non-destructive measurements, but their relatively slow scan speed and inability to reflect the chemical and physical changes within the battery limit their effectiveness. Therefore, an efficient and non-destructive detection method is required for monitoring and assessing the batteries.
In recent years, a non-destructive fault detection method based on weak magnetic field measurements of lithium-ion batteries has emerged. This method was first proposed by Ilott et al. in 2018, focusing on a non-destructive approach to study the magnetic susceptibility of batteries. The method can detect battery defects, establish a relationship between the magnetic susceptibility and charge state, and respond to differences as low as 0.1 ppm (1 μT) in susceptibilities.
In 2020, scientists from Johannes Gutenberg University (JGU) and the Helmholtz Institute Mainz (HIM) proposed a non-contact method to detect the charging state and defects of lithium-ion batteries. They used an atomic magnetometer to measure the weak induced magnetic field around lithium-ion batteries in a magnetic shielding environment, establishing a relationship between the magnetic susceptibility and the internal defects. The magnetometer in their experiment can achieve a sensitivity of 20 fT/Hz1/2. Observations from the measurements showed a decrease in the total magnetic field as the battery discharged.
Additionally, utilizing regularized magnetic field inversion, magnetic susceptibility maps corresponding to the measured field could be generated. In 2021, researchers led by Brauchle F directly measured the current distribution in lithium-ion batteries through magnetic field imaging. Using an unshielded measurement setup with anisotropic magnetoresistive (AMR) sensors, they reconstructed the battery’s current distribution based on the measured magnetic field, achieving an accuracy of 227 mA/cm2 at a local resolution of 4 mm2.
In 2022, researchers led by Bason M G from the University of Sussex utilized a magnetic flux gate array to measure the external magnetic field of batteries. Utilizing electromagnetic relationships, they extrapolated the internal current distribution within the battery, facilitating the measurement of current density on the 1 nA/cm2 scale.
To assess the accuracy of magnetic field measurements, the researchers compared the magnetic field images with those predicted by a finite element model (FEM) and they found good agreement between measured and modelled fields. Their experimental results indicated that magnetic field variations could be attributed to strain and local heating. The literature mentioned inversion methods for deriving physical quantities such as current density and magnetic susceptibility for healthy batteries.
However, research on the magnetic field distribution of the batteries with defects such as internal short circuits and cracks is scarce. Consequently, further research is necessary to enhance understanding of the magnetic field distribution in faulty battery scenarios.
Building upon previous research, this paper proposes a new solution for lithium-ion battery detection based on magnetic field detection. By coupling the battery’s P2D model with a magnetic field model, a lithium battery-magnetic field coupling model is introduced. This model can calculate the magnetic field distribution around the battery during charge and discharge processes.
By analyzing the magnetic field distribution, the health status of the battery can be inferred, enabling the detection and localization of battery faults. The study focuses on the magnetic field distribution around batteries in the presence of internal short circuits and cracks, providing valuable insights for practical measurement and detection. In addition, the magnetic field around a commercial battery pack is measured in this work, which shows the practicability of the model to a certain extent.
Model development
Researchers often build electrochemical models to study electrochemical problems. In this section, a simplified multi-physics coupling model for batteries is constructed through the application of P2D electrochemical model theory and the Biot-Savart law.
The P2D model
Generally speaking, models for lithium-ion batteries are primarily categorized into three major classes: electrochemical behavior models thermal behavior models, and aging behavior models. The electrochemical model is a mechanistic framework that employs reaction kinetics equations to describe the operational processes of the battery from an electrochemical perspective. One of the most representative models in this category is the pseudo two-dimensional (P2D) model.
The model, initially proposed by Doyle and Newman, is an electrochemical model for lithium-ion batteries based on the theory of porous electrodes. This model employs a set of partial differential equations and algebraic equation systems to describe the diffusion and migration processes of lithium ions in the solid–liquid phases within the battery, electrochemical reactions at the solid–liquid phase interface, Ohm’s law, charge conservation law, and other phenomena.
It not only accurately simulates the terminal voltage characteristics of the battery under various current excitations but also enables the simulation of the distribution of lithium-ion concentrations in the solid–liquid phases, solid–liquid phase potential distribution, and various overpotentials within the battery. The P2D model for batteries considers electrochemical reactions and the transport of lithium ions within the battery, incorporating various chemical and physical processes. Due to its higher precision, it is widely applied in research on battery capacity degradation scenarios.
As shown in Fig. 1, the model posits that the battery cell comprises a positive electrode-separator-electrolyte-negative electrode assembly, in which the electrodes are porous materials and the electrolyte is in solution. The solid component consists of electroactive material particles embedded in a conductive binder matrix. The model incorporates two dimensions: the radial direction within the positive and negative electrode particles and the thickness direction of the battery electrode plates.
Ln, Lsp, and Lp respectively denote the thickness of the negative electrode active material layer, separator thickness, and positive electrode active material layer thickness. The model posits that the positive and negative electrode active materials are regarded as uniformly distributed small spherical particles, and their motion is described using Fick’s second law. The electrolyte is filled in both the positive and negative electrode material layers (porous electrodes) and the separator region.
Figure 1
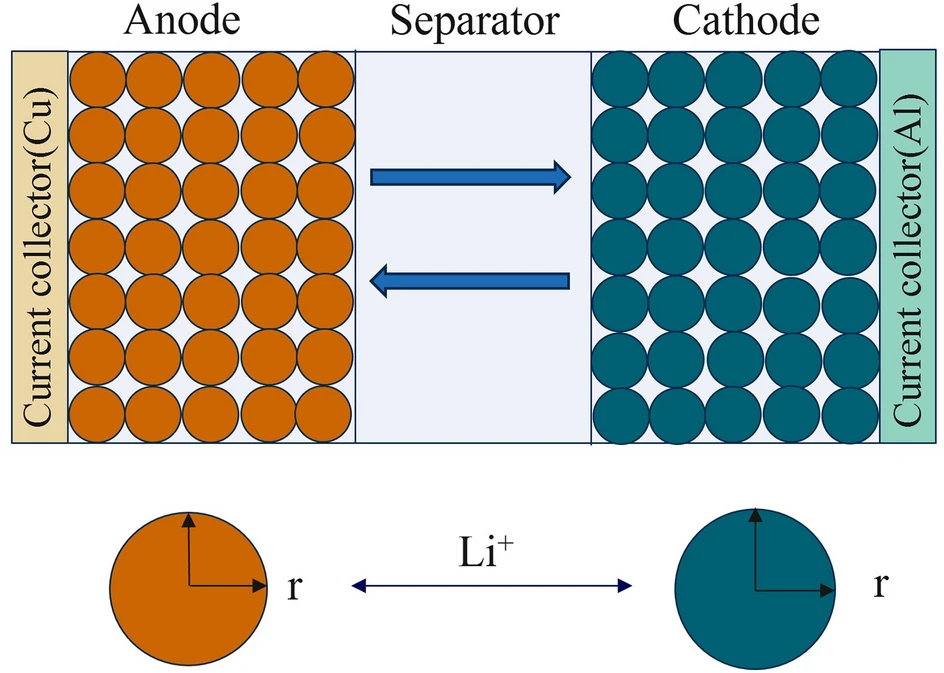
The Li-ion battery P2D model.
The premise of the model are two conservation principles: current conservation and mass conservation. Current conservation dictates that the total current is always equal to the sum of solid-phase current and liquid-phase current. Mass conservation ensures that the total amount of substance remains constant before and after any changes occur.
The cell model
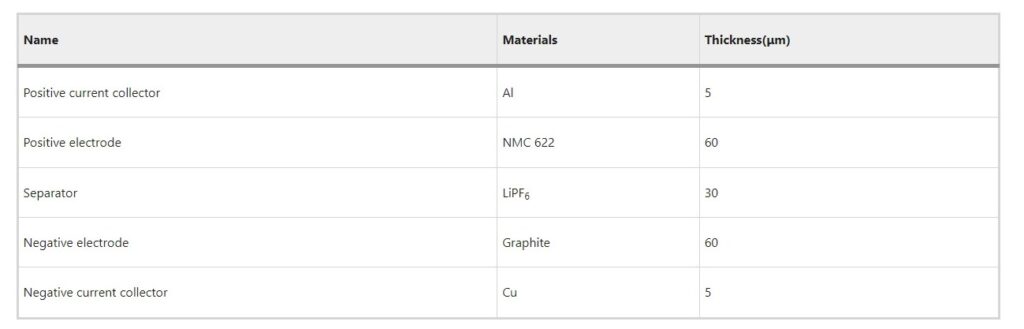
This paper establishes a multi-physics coupling model for the commercial nickel–cobalt-manganese graphite/lithium-ion battery (NMC 622). As in Fig. 2(a), this schematic illustrates the geometric structure of a three-dimensional battery model. The battery model represents a pouch cell unit with dimensions of 5 cm in length, 4 cm in width, and 160 μm in height. The cell unit consists of a positive current collector, a positive electrode, a separator, negative electrode, and a negative current collector from top to bottom, separated by a 30 μm-thick separator. The materials and thicknesses of these components are specified as shown in Table 1.
For visualization purposes, all plots are scald 10 times in the z direction due to the high aspect ratio of the geometric features. In the computation of the magnetic field, the external boundary of the cell is a rectangular air domain measuring 0.06 m × 0.09 m × 480 μm, employed to calculate the magnetic field distribution in three-dimensional space. The mesh division of the cell model is illustrated in Fig. 2b. This work is a simplified model focusing solely on the distribution of physical fields within the geometric components of the battery; therefore, the actual wiring of the battery during usage is not considered. The internal parameters used in this model are sourced from literature or the COMSOL built-in material library.
Figure 2
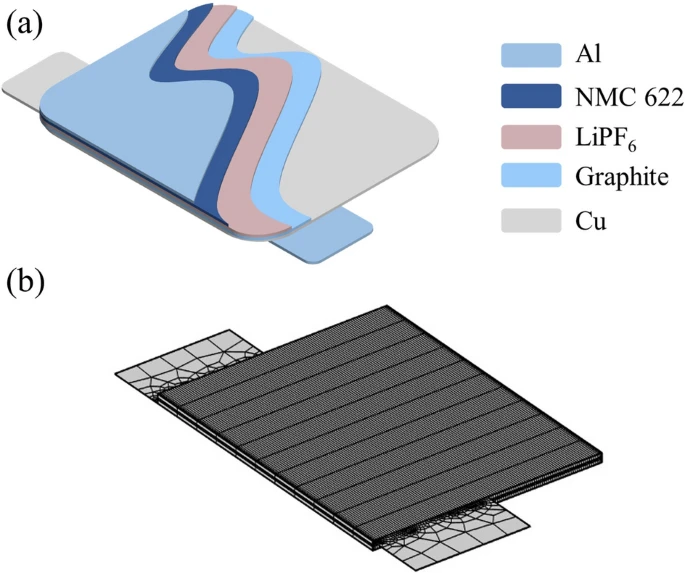
(a) Internal structure diagram of a lithium-ion pouch cell. (b) Mesh generation of the cell model.
Table 1 Basic parameters of the cell.
Results and discussion
This work establishes a lithium-ion cell model by coupling a P2D battery model with a magnetic field model. The model characterizes electrochemical quantities such as voltage distribution within the lithium-ion battery and the corresponding magnetic field distribution of the cell. In this section, we examine the magnetic field distribution associated with internal short circuits in the cell as well as the magnetic field distribution with cracks.

