Part 2: Flawless cells, Internal short circuit
Flawless cells
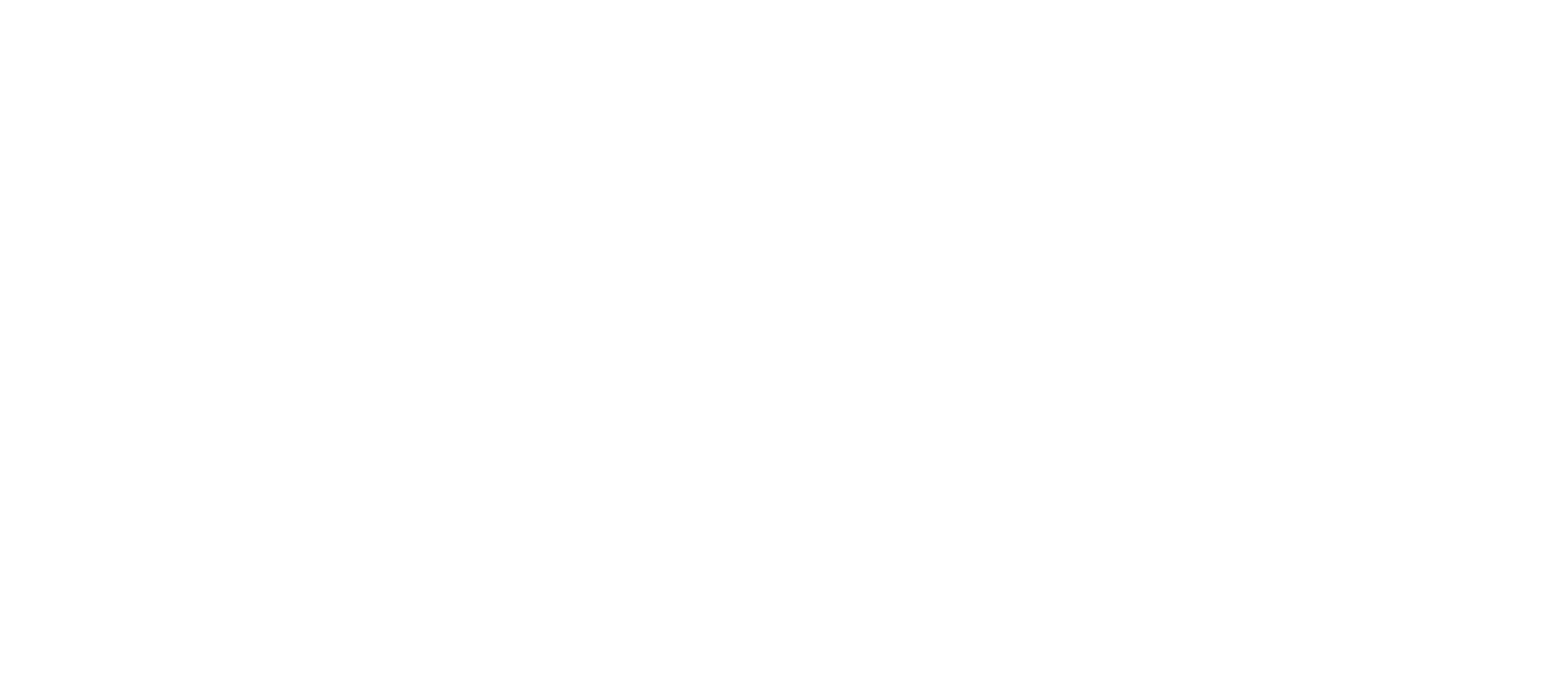
First, we conducted calculations for the potential distribution, current density distribution, and surrounding magnetic field of a healthy battery. Figure 3 illustrates the potential, relative current density, and magnetic field distribution during the charging process under 4 V 1C condition. As in Fig. 3a, a non-uniform voltage distribution within the current collector is clearly observed.
The voltage near the ground terminal is lower than the average voltage, while the voltage near the input ground terminal is higher than the average voltage. Consequently, the non-uniform voltage distribution results in a non-uniform distribution of current during the charging process.
Figure 3
(a) Voltage distribution in the positive current collector of a flawless battery during the charging state. (b) Relative current density distribution in the separator of a flawless battery during the charging state. (c) Magnetic field distribution diagram of a fault-free battery during the charging state.
The simulated results of current density distribution of the flawless cell at the middle of the separator at the beginning of the 1C charge are illustrated in Fig. 3b. In the design of lithium-ion battery pouch cell, all current exits the cell on the cell “tabs”, resulting in higher current density near the positive and negative electrode tabs. As the charging process progresses, the current density in the central portion of the cell increases. The non-uniformity in current density distribution leads to an uneven distribution of the magnetic field within the cell.
As in Fig. 3c, for the charging condition of 4 V 1C, the magnetic field component images on the upper air domain surface are presented at the beginning of cell charging. According to the Biot-Savart law, the distribution of the magnetic field depends on the distribution of the current.
As can be seen that due to the instability of the current, the cell will generate a corresponding magnetic field in the surrounding space. Since the current flows from the positive collector, the current density is higher at the collector, and accordingly, the magnetic field is higher here. From the simulation results, it is evident that during normal battery operation, the magnetic field generated by the current on the designated air domain surface ranges approximately from 1 to 4 μT, with a maximum reaching 4.6 μT.
Internal short circuit
Battery thermal runaway refers to the phenomenon of rapid overheating within a battery characterized by an exothermic chain reaction occurring internally, leading to a drastic change in the rate of temperature rise. When a battery experiences a short circuit due to external impact or internal faults, the Ohmic heating generated by the short-circuit current leads to overheating of the battery, resulting in thermal runaway.
Internal short circuit refers to the phenomenon where the separator within a battery is damaged or compromised, resulting in a direct connection between the positive and negative electrodes of the battery. The primary causes of internal short circuit faults are threefold: electrical abuse, mechanical abuse, and thermal abuse. Mechanical misuse and thermal misuse can be mitigated through the implementation of standardized battery production and usage practices, whereas electrical misuse cannot be entirely avoided through these means.
Electrical misuse is primarily induced by short circuits, overcharging, or over-discharging. In the case of a short circuit, the discharge current of the battery is substantial, generating a significant amount of polarization heat and Ohmic heat, resulting in the melting of the separator and the establishment of an internal short circuit by connecting the positive and negative electrodes. Overcharging and over-discharging, on the other hand, lead to the deposition of lithium and copper on the negative electrode. The accumulation of lithium and copper forms metal dendrites, which, with continued reaction, may penetrate the separator, causing an internal short circuit within the battery.
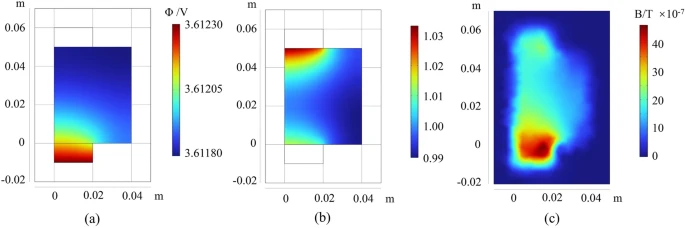
Based on the lithium-ion cell model established in the preceding section, this section introduces a short circuit point in the physical model and constructs a coupled multiphysics model electrochemistry-magnetic field-thermal coupling. The designated short circuit point is located at x = 0.02 m, y = 0.02 m, with a dendrite radius set at 50 μm. As shown in Fig. 4a, when an internal short circuit occurs in the battery, the positive and negative electrode materials are connected through the dendrite.
It is assumed that the shape of the lithium dendrite is a cylinder with the same height as the separator in this work. At the same time, electrochemically inactive regions are set in both the positive and negative electrode domains to enhance the convergence of the model. The schematic of the mesh partition for the model is presented in Fig. 4b. Due to the significant temperature and magnetic field gradient changes in the short circuit region, the mesh is refined in the corresponding areas.
Figure 4
(a) Schematic diagram of the internal short circuit of the LIB caused by the penetration of lithium dendrites through the separator. (b) The grid division diagram when internal short circuit is caused by dendrites.
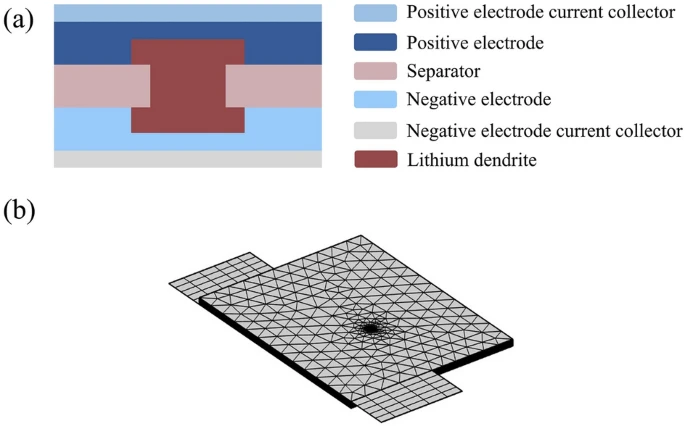
Figure 5 presents simulation results of the magnetic field distribution around the short-circuit region in a battery with 50 μm dendrites at 0 s, 0.001 s, 0.01 s, and 0.1 s following the occurrence of an internal short circuit within the battery’s 5-layer cells. Given that the dendrite radius is significantly smaller than the geometric dimensions of the battery, the magnetic field distribution in the dendrite region is magnified for ease of observation.
From the figures, it is evident that in the vicinity of the lithium dendrite, there is a pronounced increase in the magnetic field. Simultaneously, the highest magnetic field is observed at the dendrite position, and the magnetic field variation is confined to a small space near the dendrite. In a normally operating battery, internal current flows from the negative electrode to the positive electrode.
As the lithium-ion battery undergoes charging and discharging cycles during the electrochemical reactions within the liquid electrolyte, excess lithium ions combine with electrons transported from the negative electrode when the embedded lithium content in the graphite exceeds its capacity. Due to factors such as uneven current density and lithium-ion distribution, lithium ions unevenly deposit on the surface of the negative electrode, forming lithium dendrites. Once the lithium dendrite grows to a certain extent, it can penetrate the separator, causing an internal short circuit in the battery.
At the onset of internal short circuit, the current flows along the lithium dendrite from the positive electrode to the negative electrode. The lithium dendrite acts as a conductor, resulting in a significant abnormal increase in short-circuit current. Correspondingly, the magnetic field at the short-circuit location also exhibits an abnormal increase.
Figure 5

The simulated distribution of regional magnetic field near lithium dendrites at different time (50 μm): (a) 0 s; (b) 0.001 s; (c) 0.01 s; (d) 0.1 s.
The magnetic field distribution images on the surfaces of the positive and negative electrodes are illustrated in Fig. 6. At 0.01 s after the short circuit, a distinct phenomenon of increased magnetic field is clearly observable on the battery surface, particularly at x = 0.02 m, y = 0.02 m, where the anomalous magnetic field value is approximately 5 μT larger than in other regions. In the operational lifespan of commercial batteries, internal short circuits are not directly observable from the outside.
However, this phenomenon allows us to employ magnetic flux sensors and other magnetic measurement devices for battery diagnostics. By detecting the abnormal increase in the magnetic field, the number of fault points can be determined, and the fault locations can be identified to ensure the safe use of the battery.
Figure 6
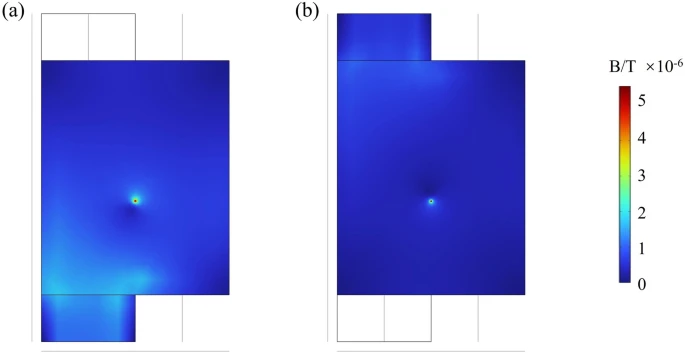
The magnetic field distribution on the surface of the battery at 0.01 s following the short circuit: (a) positive electrodes; (b) negative electrodes.
Figure 7 shows the results of the maximum magnetic field values in the system after the occurrence of internal short circuits induced by lithium dendrites with different radius. The dendrites can be considered as cylindrical lithium metal conductors with constant material properties and height. The resistance of the dendrites decreases as the base area increases, leading to an increase in short-circuit current with the growing radius of the lithium dendrites. According to the Biot-Savart law, as the current in the short-circuit region increases, the corresponding magnetic field values also increase.
When the dendrite radius is 50 μm, the maximum magnetic field value in the system is approximately 55 μT. When the dendrite radius increases to 100 μm, the maximum magnetic field value in the system reaches about 75 μT. Therefore, by detecting the magnetic field values of the battery, we can not only determine the position of the dendrites but also estimate the size of the dendrite radius.
It is worth noting that, due to the magnitude of the maximum abnormal magnetic field values being comparable to the Earth’s magnetic field (approximately 50–60 μT), under the measurement conditions where the Earth’s magnetic field serves as the background field, a clear distribution of abnormal magnetic fields can also be detected.
Figure 7
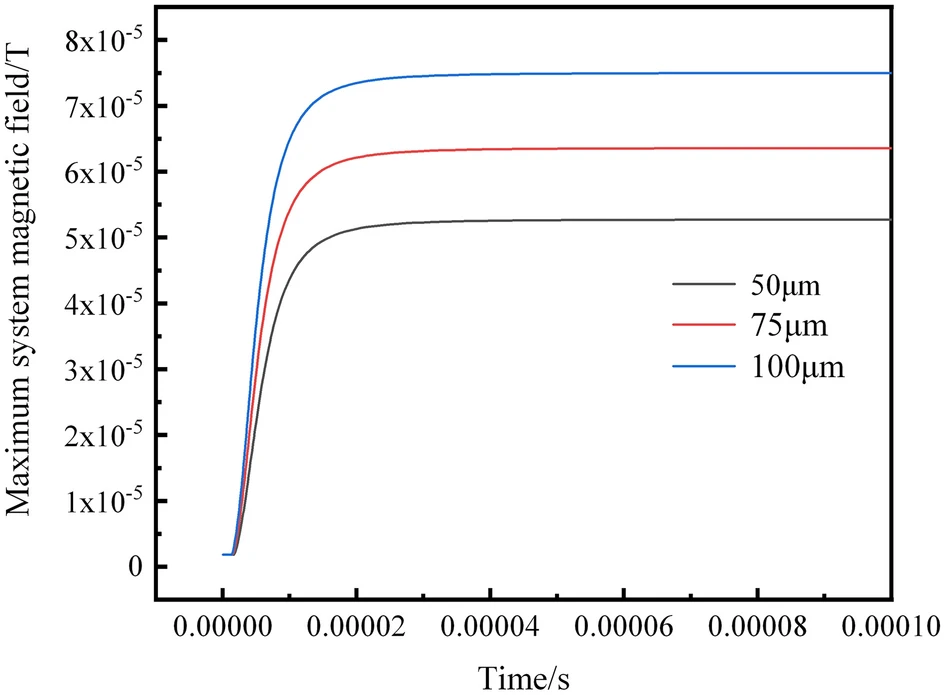
The maximum magnetic field of the simulated system for different dendrite radius.
The temperature elevation in the battery structure is directly correlated with the internal flow of current. Therefore, the lithium dendrites exhibit an initial temperature increase, and the surrounding structure gradually experiences elevated temperatures with the lithium dendrite at the center.
The primary sources of heat generation during the internal short circuit process include reversible entropy heat and irreversible polarization heat from electrochemical reactions occurring on the positive and negative electrodes, Joule heat generated by lithium ions embedding and stripping within the positive and negative electrodes, and Joule heat generated when electrons pass through the positive and negative current collectors and the lithium dendrite.
The result of temperature distribution in the 5-layer cells near the short-circuit region is illustrated in Fig. 8. At 0 s, the initial temperature of the lithium dendrite is the same as the ambient temperature, which is 293.15 K. By 0.001 s, the highest temperature near the lithium dendrite rises to approximately 295 K.
At 0.01 s, the maximum temperature in the short-circuit point area reaches around 315 K. Following a short circuit fault in the battery, the maximum temperature is achieved within 0.1 s, reaching approximately 315 K. Additionally, it can be observed that the temperature rise area of the negative electrode material is significantly larger than the corresponding area on the positive electrode material. This is attributed to the lower specific heat capacity of the negative electrode. Correspondingly, within the time frame of 0.1 s, the system’s highest temperature occurs in the region near the negative electrode surface adjacent to the lithium dendrite.
Figure 8
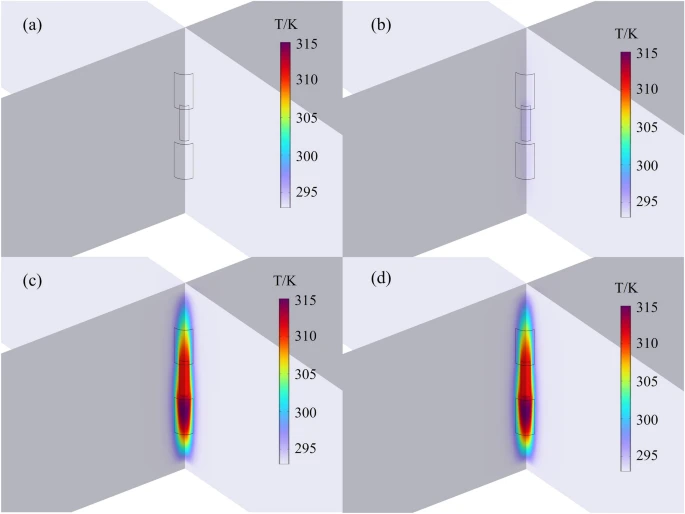
The simulated distribution of regional temperature near lithium dendrites at different time (50 μm): (a) 0 s; (b) 0.001 s; (c) 0.01 s; (d) 0.1 s.
During an internal short circuit of a battery the two electrode materials are internally interconnected electronically, leading to a localized increase in the current density. This results in excessively high local temperatures and the consequential damage to the battery. In severe cases, it may even lead to fire incidents.
The abnormal distribution of current can cause an anomalous distribution of the magnetic field, making fault diagnosis of internal short circuits feasible through magnetic field detection methods. Another commonly used approach by scientists in the study of internal short circuit faults is the temperature detection method. However, due to the relatively slow temperature response, measurements may introduce inaccuracies13.
The variation over time in the maximum magnetic field values and maximum temperature values of the simulated system is shown in Fig. 9. The results evident that within an extremely short time after the occurrence of a short circuit fault, both the maximum magnetic field and temperature values in the system experience a rapid increase.
The magnetic field response precedes the temperature response, with the maximum value of the system’s magnetic field reaching approximately 5.25 × 10-5 T in less than 0.001 s, after which the system’s maximum magnetic field value changes tend to stabilize. In contrast, the system’s maximum temperature value takes about 0.1 s to reach 315 K and then stabilizes. Therefore, under internal short circuit conditions, using magnetic field detection for state monitoring and health assessment of the battery is a superior method.
Figure 9
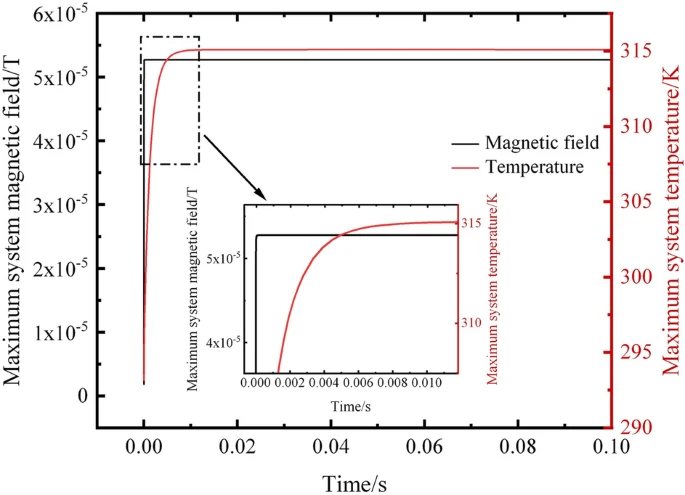
Variation of the maximum magnetic field and maximum temperature over time.